Modelling the Earth System and the dynamics of complex systems for understanding climate change - The Nobel Prize in Physics 2021
Jürgen Kurths | Potsdam Institut für Klimafolgenforschung, Berlin.
___________________________________________________________________________________________
The Nobel Prize in Physics 2021 was awarded to Syukuro Manabe, Klaus Hasselmann and Giorgio Parisi “for groundbreaking contributions to our understanding of complex systems” including major advances in the understanding of our climate and climate change. The CAFE project celebrates their achievement with a blog article highlighting their main contributions to climate research.
This year’s Nobel Prize in Physics recognized that our knowledge of Earth’s Climate, one outstanding example of a complex system, rests on a solid scientific foundation of physics, mathematics and complex systems science. The key to understanding the concept of predictability is to understand the underlying causes of variability. Only then we can understand the stark reality of global warming and the role of human activity on it.
Complexity is intrinsic to nonlinear physical systems, from atomic to planetary scales. A complex system comprises various interacting components. Physicists have typically attempted to describe them mathematically over the past two centuries by studying the individual components separately. However, new properties emerge at each level of complexity as a consequence of the interplay of (dis)order and fluctuations. Similarly to the chaotic nature of weather, where small deviations in initial conditions result in huge differences at a later stage, noise-induced variability can determine the fate of some nonlinear dynamical systems. This year’s Nobel Laureates have made seminal contributions to the study of complex phenomena, making substantial advances to the understanding of complex interactions in the Earth’s Climate system.
One half of the Physics Nobel Prize 2021 was awarded jointly to Syukuro Manabe (Princeton University, USA) and Klaus Hasselmann (Max Planck Institute for Meteorology, Hamburg, Germany) for their pioneering work on the physical modelling of Earth’s climate, quantifying variability and predicting global warming due to carbon dioxide (CO2) increase in the atmosphere, while the other half was awarded to Giorgio Parisi (Sapienza University of Rome, Italy) for his discovery of the interplay of noise-induced fluctuations and (dis)order in physical systems.
Advent of a new era in climate modelling
After receiving his PhD in 1958 from the University of Tokyo, Syukuro Manabe continued his career in the United States as a researcher at the Geophysical Fluid Dynamics Laboratory of National Oceanic and Atmospheric Administration (NOAA), working on numerical weather prediction. At that time, weather forecasting was mainly treated as an empirical problem: studying weather maps and trying to predict the weather by extrapolating forward. Manabe believed that equal emphasis should be placed on both understanding as well as predicting climate change. He tried to find a relation between the increase in global temperature with that of the level of CO2 in the atmosphere. Research in this direction had already been started several decades ago from a rather global consideration by yet another Nobel Laureate, Svante Arrhenius (Chemistry Nobel Prize 1903) who understood the role of greenhouse gases in the atmosphere which absorbed the long-wave radiation emitted from the Earth’s surface, thereby maintaining the Earth’s temperature at the observed value.
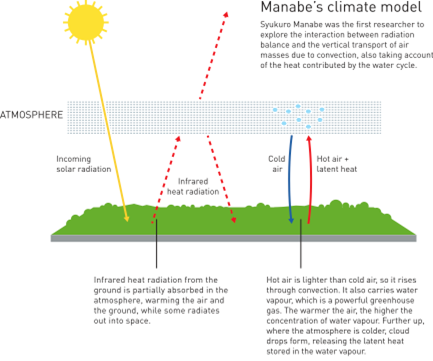
Manabe realized that the heating of the Earth’s surface would warm the air in close contact with the Earth’s surface, generating convection. Consequently, warm air (water vapour) would rise and, when meeting the cooler upper layers of the atmosphere, release its heat in the form of latent heat. Taking this convective adjustment into consideration, Manabe and Wetherald (1967) modelled the atmosphere as a one-dimensional vertical column with an initial profile of relative humidity and greenhouse gases. This profile evolved with time according to the dynamics of radiative transfer and upward convection of water vapour (see Figure 1). They found that although the change in oxygen and nitrogen levels has a negligible impact on temperature, doubling the CO2 concentration leads to an increase in the global temperature by 2.36°C, while the temperature in the stratosphere substantially decreases (see Figure 2). It is interesting to note that the British engineer Guy Callendar (1938) discovered the potential impact of anthropogenic CO2 emission into the atmosphere on the global climate through a simple radiative energy balance model of the Earth’s surface. Although Fritz Möller, one of Manabe’s collaborators, noted serious flaws in Callendar’s approach, Manabe realised that his radiative-convective model was an excellent conceptual tool to study the greenhouse effect. Even with hundreds of hours of (at that time) very expensive computational time required to run these models, it is fascinating that Manabe’s rather simple 1-D model was able to quantify climate sensitivity more accurately than the highly complex General Circulation Models (GCMs) that were used at that time. His findings remain valid even today, making his paper the most influential climate change paper of all time, as based on a recent survey by CarbonBrief.
Figure 1. Manabe’s radiation-convective climate model. Johan Jarnestad / Royal Swedish Academy of Sciences.
Proceeding one step further, Manabe incorporated effects of hydrology at Earth’s surface in a three-dimensional GCM with 9 vertical layers resolving the atmosphere from the surface boundary layer till the stratosphere (Manabe and Bryan, 1969), and later, coupled an atmospheric model with a mixed-layer oceanic model (Manabe and Stouffer, 1980). He then continued improving the models by increasing their resolution and the number of equations. These advances brought additional insights about the Earth’s complex interactions. In 1975, they (Manabe and Wetherald, 1975) simulated for the first time the three-dimensional response of the hydrological cycle and temperature to increased CO2 concentrations in the Earth’s atmosphere, and found that the doubling of CO2 significantly intensifies the hydrologic cycle of the model. In 1980, they (Manabe and Stouffer, 1980) were able to show that around the Arctic Ocean the warming of the atmosphere surface layer would be much larger in winter than in summer, becoming an instructive example of complex interactions. Later, Manabe and his colleagues, based on their simulations, demonstrated an interhemispheric asymmetry in temperature changes under an increase of CO2 and how it is affected by oceanic processes (Stouffer et al., 1989): the warming of surface air was predicted to be faster in the Northern Hemisphere than in the Southern Hemisphere. At the same time, the warming over the northern North Atlantic was predicted to be relatively slow because of the weakening of the large-scale ocean circulation (thermohaline circulation) which acts as a countereffect.
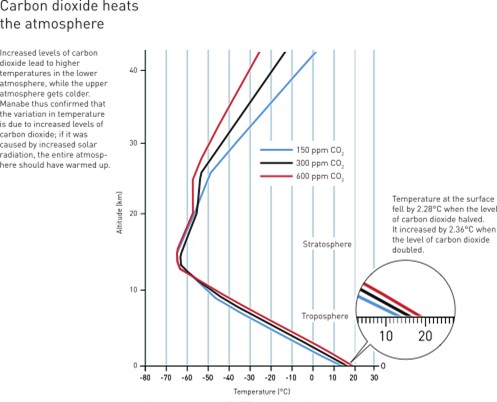
Figure 2 The effect of C02 concentration changes in the Temperature of the Earth at different altitudes. Johan Jarnestad / Royal Swedish Academy of Sciences / Manabe & Wetherald (1967), Journal of the Atmospheric Sciences
The “red noise” problem in climate signals
Large differences in weather patterns are observed all around the planet. The uneven spatial and temporal distribution of solar radiation (due to the shape of the Earth, its orbit around the Sun, and the tilt in its axis), is the main driving factor of the complex dynamical processes in the atmosphere and oceans. Although in principle a precise knowledge of the current state of the system and its governing equations allows determining the state at some later time, in reality it is impossible to precisely predict the values of climate variables like air temperature, pressure, humidity, wind speed, etc., from our observations. As the equations describing climate processes are nonlinear, small uncertainties in the initial state propagate as large errors in predictions. The chaotic nature of weather (referring to its sensitivity to initial conditions) was first discovered by the American meteorologist Edward Lorenz in 1963. Therefore, the question that attracted much interest was: How can we quantify, in deterministic climate models like that of Manabe and others, the variability in climate predictions that is due to the chaotic nature of the weather system?
During the period in which Manabe developed his model, Klaus Hasselmann (Ph.D. 1957 from the University of Göttingen) worked on developing models of ocean waves and understanding the complex air-sea interaction processes at the ocean-atmosphere interface (Hasselmann 1966, 1967, 1991). His struggles with turbulence theory already as a Diploma student in Hamburg and later as a doctoral student in Göttingen taught him a lot on stochastic processes and interactions in nonlinear systems, which built his intuition and enabled him to solve problems later on. Hasselmann created a stochastic climate model in which he ingeniously incorporated the rapid fluctuations in climate due to weather as ‘noise’ (Hasselmann 1976). He attributed the variability of climate to internal random forcing by short time scale ‘weather’ components of the system. He drew a parallel between the response of the climate system and the random walk characteristics of large particles interacting with an ensemble of much smaller particles exhibiting Brownian motion, exploiting a theory originally proposed by Albert Einstein in 1905. His model was in very good qualitative agreement with the ‘red’ spectra observed in climate signals (Figure 3; Hasselmann 1977), i.e. he was able to solve the long standing “red noise” problem in climatology. Hasselmann’s approach to include stochasticity in the climate model set a benchmark for climate scientists to address variability. It paved the way for modelling the dynamics of the climate system, by taking into account interaction of oceans with other complex sub-systems, such as the atmosphere, the air-sea interface and the carbon cycle.
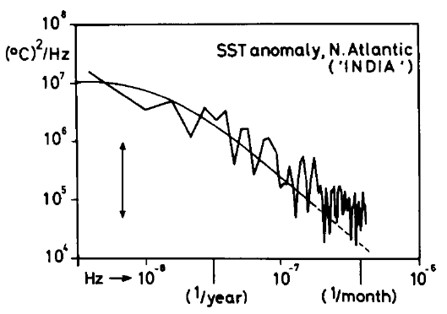
Figure 3 The first application of Hasselmann’s Stochastic climate model to climate data. Spectrum of Sea Surface Temperature (SST) anomaly at Atlantic Ocean Weather Ship India for the period 1949-1964. The arrows indicate 95% confidence interval. The smooth curve was calculated from the stochastic two-scale model of SST variability. The frequency spectra of large-scale, long-time SST anomalies exhibit a red noise behavior (inverse square law) in time scales intermediate to the response times of weather and climate. Therefore, they may be explained naturally as the response of the oceanic surface layers to short-time-scale atmospheric forcing. Frankignoul & Hasselmann (1977), Tellus 29.
The positive role of noise in understanding climate change
Statistical data analysis of climate records indicates the occurrence of major climate changes with an apparent periodicity of 100,000 years, which roughly corresponds to the alternation between glacial and interglacial stages. Milankovitch in 1930 related these periodic changes to the variations in the Earth’s orbital parameters, thus associating climate change with external astronomical forcing. However, actual calculations show that the eccentricity of the Earth’s orbit is too small to account for temperature variations of the order of 10 °C as observed in paleoclimatic records. This gave rise to the hypothesis that the cycle may arise from an internal mechanism due to atmospheric and oceanic circulations which could then have a nonlinear response to external forcing. Giorgio Parisi and his collaborators in the early 1980s, solved the above problem using the concept of ‘stochastic resonance’, a phenomenon observed in nonlinear physical systems like the Earth’s climate wherein the combination of an external periodic perturbation with a certain amount of noise can amplify the signal-to-noise ratio thereby favoring a particular outcome. Influenced by Hasselmann’s (1976) idea of modelling climate variability due to short time-scale phenomena as stochastic perturbations (noise), their model (Benzi, Parisi et al., 1982, 1983) described the 100,000-years cycle as an effect arising from the combination of the noise induced by the internal dynamics of the atmosphere and ocean with the external forcing due to the periodic variations of Earth’s orbit.
Detecting climate change due to human impact
Later in his career, Hasselmann turned his focus to distinguish human-induced climate change from the natural variability observed in climate data. He noted that while the predictions of the state-of-the-art coupled ocean-atmosphere GCMs showed a surmountable qualitative and circumstantial evidence of global warming due to an increase in greenhouse gas emissions, there was a substantial lack of a framework to quantitatively measure this effect. Between 1979 and 1997, Hasselmann invented a technique to systematically compare the spatiotemporal dynamics in climate models and observations (Hasselmann 1979, 1993, 1997). He found that the data from models and observations contain sufficient information about the properties of noise and signals. Different phenomena, such as changes in solar radiation, volcanic activity, or concentration of greenhouse gases, leave unique imprints in the climate signal, which can then be separated. His ‘optimal fingerprinting’ method, not only successfully detected signals of climate change but also distinguished effects of humans on the climate system from those due to natural causes (Figure 4; Hegerl et al. 1997, 2011, Barnett et al. 2005).
An early climate activist in science, Hasselmann’s work laid the foundations for further studies in climate change with his fingerprint approach which continues to be widely used by climate researchers today.
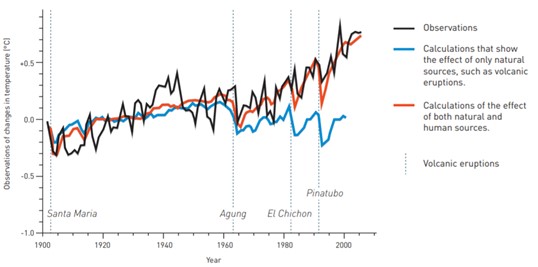
Figure 4. Hasselmann developed the Optimal Fingerprinting method for discerning traces of human impact on atmospheric heating from that due to natural causes. Comparison between changes in mean temperature (in °C) with respect to the average for the period 1901-1950, Johan Jarnestad / Royal Swedish Academy of Sciences / Hegerl & Zweirs (2011), WIREs Climate Change.
Legacy for new discoveries and future advances
Over the years, state-of-the-art climate models have improved tremendously, thanks to unprecedented advances in computer science and computing power, and also, a massive amount of ground-based and satellite observations that have allowed gaining a much better understanding of the complex interactions between different components of the Earth’s climate. The pioneering works of Syukuro Manabe and Klaus Hasselmann established the pillars on which models for numerical weather prediction stand today. In fact, such numerical models are the key elements of the very recent “Destination Earth” initiative, which aims to simulate the Earth’s weather and climate with an unprecedented spatiotemporal resolution, promising much better forecasts of extreme weather events, and improved understanding of climate change impacts.
The recognition of climate science and complex systems by the Nobel committee comes at a time when the world is battling a climate crisis. The groundbreaking works of Syukuro Manabe, Klaus Hasselmann and Giorgio Parisi have provided definite answers to profoundly important questions related to the past, present and future of our planet and our role in it. It is fascinating that they were able to make such incredible advances with the limited computational resources available in the 1960s-1970s. Just for a comparison, a simple mobile phone nowadays is much more powerful than the best computers at that time. How much more would they have discovered half a century ago, if the current computational resources were available? Let your imagination run wild!
Further reading
- Manabe, S., Wetherald, R.T., 1967. Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity. J. Atmospheric Sci. 24, 241–259. https://doi.org/10.1175/1520-0469(1967)024<0241:TEOTAW>2.0.CO;2
- Manabe, S., Stouffer, R.J., 1980. Sensitivity of a global climate model to an increase of CO2 concentration in the atmosphere. J. Geophys. Res. Oceans 85, 5529–5554. https://doi.org/10.1029/JC085iC10p05529
- Benzi, R., Parisi, G., Sutera, A., Vulpiani, A., 1982. Stochastic resonance in climatic change. Tellus 34, 10–15. https://doi.org/10.3402/tellusa.v34i1.10782
- Hasselmann, K., 1976. Stochastic climate models Part I. Theory. Tellus 28, 473–485. https://doi.org/10.1111/j.2153-3490.1976.tb00696.x
- Hasselmann, K., 1993. Optimal Fingerprints for the Detection of Time-dependent Climate Change. J. Clim. 6, 1957–1971. https://doi.org/10.1175/1520-0442(1993)006<1957:OFFTDO>2.0.CO;2